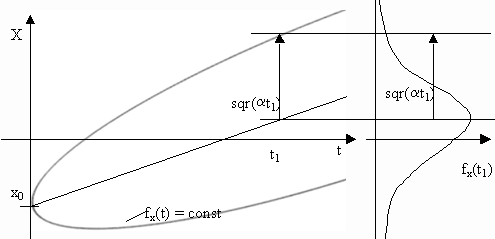
In many applications a drift components is added to the Brownian motion.
The easiest example is a random walk where the step to the left is of a different likelihood that to the right. . This results in a mean value which is no longer zero.
The stochastic differential equation adds a deterministic drift term to the diffusion term of the Wiener process. b denotes the drift coefficient.
The solution of the above stochastic differential equation is the Wiener process with drift:
y(t) can be seen as a stochastic variable. Realizations of y(t) are representations of the process. The expectation value for y(t) and ln y(t) can be compute as shown below.
The first order expectation value for y(t) is as following:
y0 represents the displacement a t0.
The probability density function for y(t) is the gaussian distribution with a mean value (y0+b t) and a time dependent variation a t.
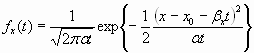
The figure below demonstrates the evolution of the distribution function over time.
